Regression using neural networks

Classification

Neural networks are powerful learning models from machine learning that can learn even complex patterns from data. They are commonly used for various classification tasks, such as identifying objects in images or predicting sentiments in text. But what if we want to use neural networks for regression tasks, such as estimating home prices or forecasting company sales? How can we adapt neural networks to handle continuous outputs instead of discrete outputs? In this blog post, we will address these questions and present some of the options and techniques available for using neural networks for regression tasks.

Regression as a task

Basically, regression is about approximating a function as accurately as possible by another function. This can have various reasons, e.g. the evaluation of the function to be approximated may take too long (this is the case with neural network performance after training), the function is too complicated or a number of other reasons.

Regression is also called regression analysis according to Wikipedia. In the following, however, only the term regression is used here. ¹

One regression method is the method of least squares ², where at each data point the error between the original function $f$ and the replacement function $f^*$ is calculated, squared, and summed over all data points:

The total error here is $e$. In the formula $n \in \mathbb{N}$ denotes the total number of data points. The task of a corresponding regression algorithm is now to minimize the corresponding error:

Loss-Metric

There are many different loss metrics to calculate corresponding errors in the data.

1. Mean Absolute Error: In this case the error is classically

computed.

2. Mean Squared Error: Here, the error is calculated and then squared

3. Mean Squared Logarithmic Error: Here the error is logarithmized and then squared

There are a number of other loss metrics. A listing can be found here.

In the following, Mean Squared Error is used. This is a good basis and often leads to good results. Sometimes other error functions can give better final results, but this depends on the problem.

Implementation using Tensorflow

In the following, a simple regression task is to be solved. Here a sine function

on the range $x \in [0, 1]$ can be approximated using a neural network. The sine function is well suited to this example, since the sine function only changes in the range

and is thus normalized. This sine function is visualized below:

Generation of the data set

Before a dataset can be created, imports are necessary for later work:

import numpy as np
import tensorflow as tf
import tensorflow.python.keras.metrics as tfm

import math

from tensorflow.python.keras import Sequential
from tensorflow.python.keras.optimizer_v2.adam import Adam
from tensorflow.python.keras.layers import InputLayer, Dense
from tensorflow.python.keras.losses import MeanSquaredError

Then we define a function in which the sine function is evaluated.

def function_eval(x: float):
  return math.sin(2*math.pi*x)

Now we generate $100$ equidistant points on the interval $[0,1]$ as training data set and $200$ equidistant points on the identical interval as test data set.

## Training Dataset
x = np.linspace(0, 1, 100)

y = []
for i in range(x.shape[0]):
  y.append(function_eval(x[i]))

y = np.array(y)

## test Dataset
x_eval = np.linspace(0, 1, 200)

y_eval = []
for i in range(x_eval.shape[0]):
  y_eval.append(function_eval(x_eval[i]))

y_eval = np.array(y_eval)

Here with we have all necessary data to perform an appropriate training with a neural network.

Training the model

Next, we define a corresponding neural network:

model = Sequential([
      InputLayer(input_shape=(1)),
      Dense(units=64, activation="relu"),
      Dense(units=192, activation="relu"),
      Dense(units=256, activation="relu"),
      Dense(units=256, activation="relu"),
      Dense(units=1, activation=None)
])

This neural network configuration arose from hyperparameter optimization. However, smaller or guessed neural networks also work very well for this regression task.

Next, the respective optimizer, the loss function and the metric have to be defined:

optimizer = Adam(learning_rate=1e-4)
loss = MeanSquaredError()
model.compile(optimizer=optimizer, loss=loss, metrics=tfm.MeanSquaredError())

Now the neural network can be trained.

model.fit(x, y, epochs=100)

As a final step, the neural network can still be evaluated to find out the error and accuracy on the test data set:

results = model.evaluate(x_eval, y_eval, verbose=0)
print("Test loss, test accuracy: ", results)

There are two equal results here because MeanSquaredError was used for both the error and the accuracy. An alternative for the accuracy would be MeanAbsoluteError..

Visualization of the results

The neural network from above was trained by us for different numbers of epochs. A comparison between the actual function to be approximated and the output of the neural network is visualized below:

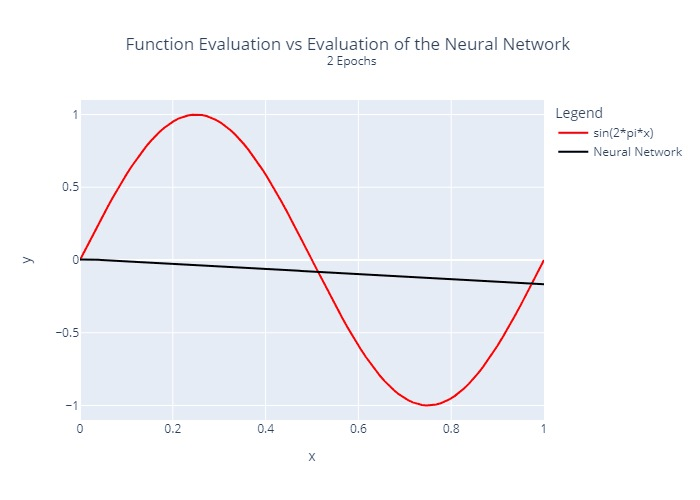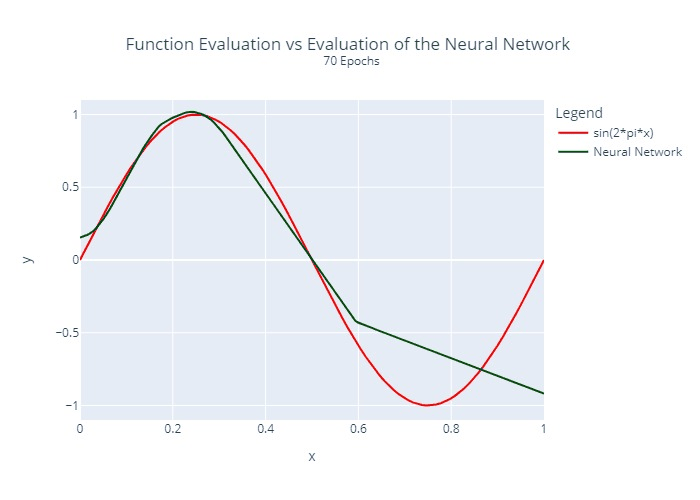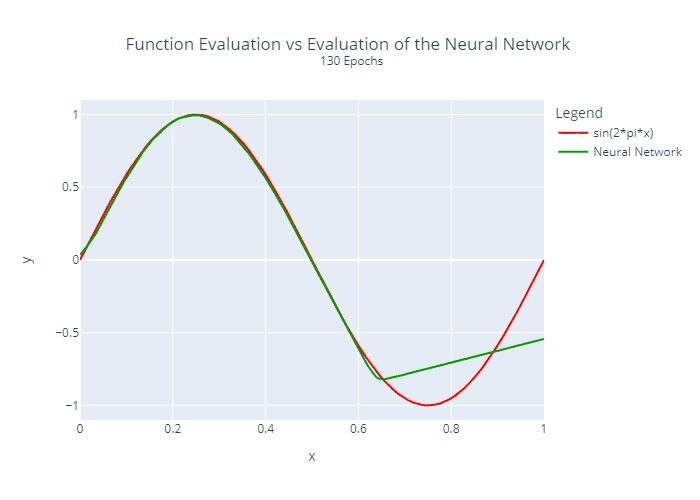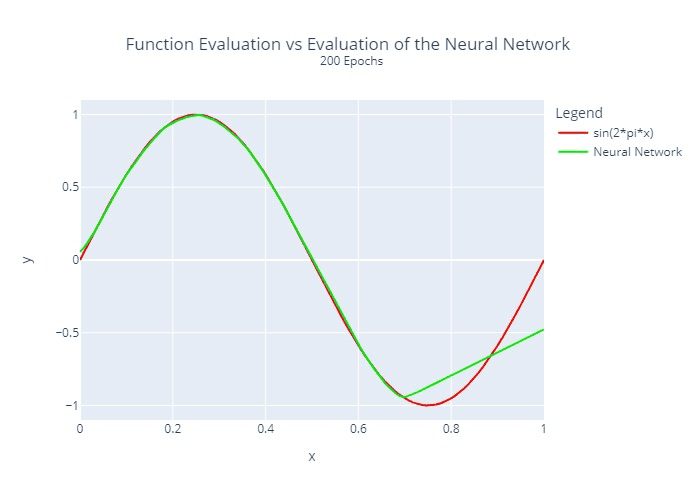
Furthermore, we calculated and plotted once the squared error at each location for each epoch:

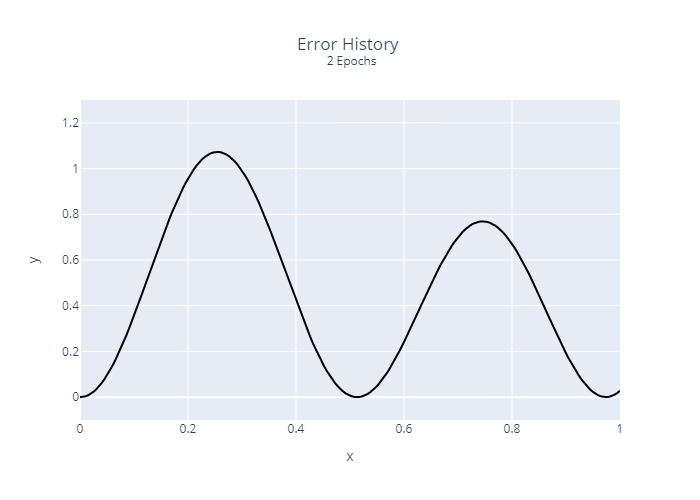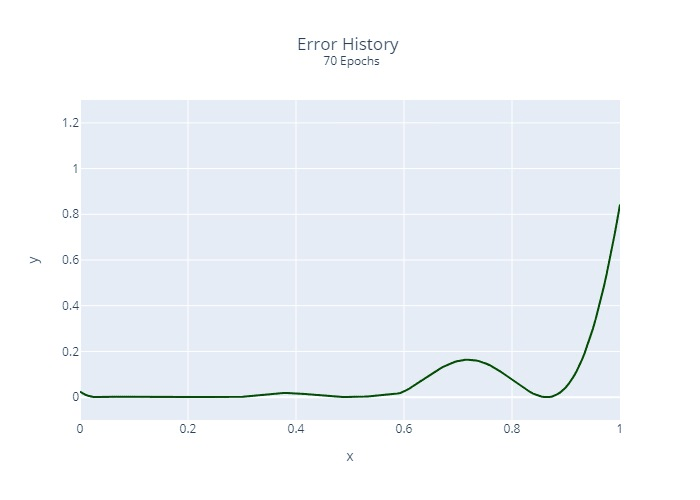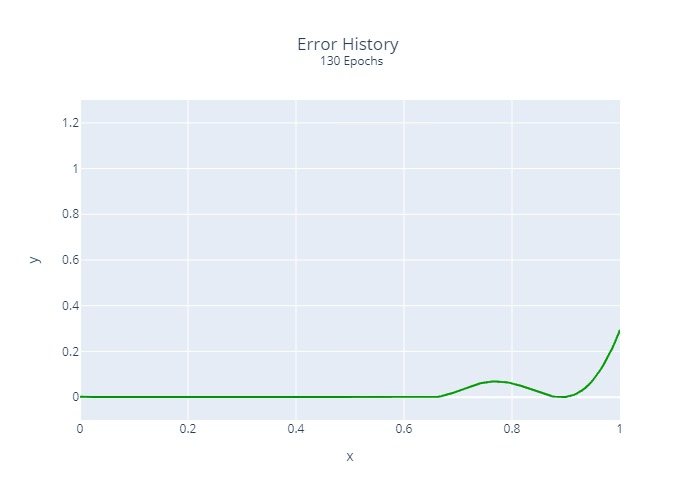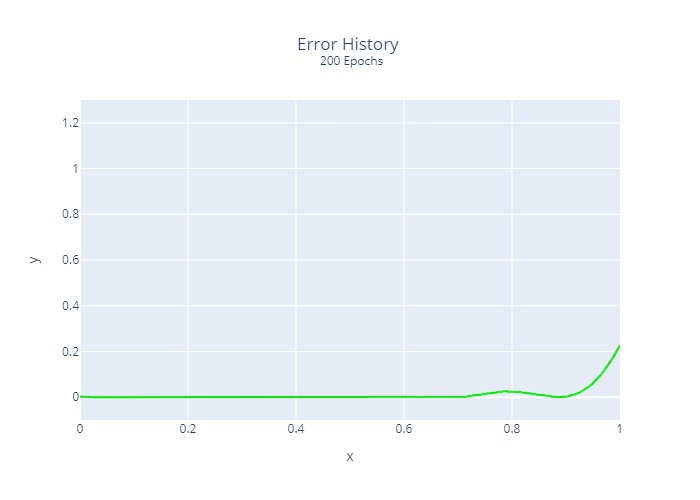
It is relatively clear that the regression does not converge at the same rate at all points. This is a common problem with many regression algorithms.

This example was a relatively simple example. Often the dimensions of both the input and output data are significantly higher. Accordingly, a learning process can require more time due to the higher complexity of the data set.

Notes

As shown above, neural networks are suited for use in regression problems. However, it is important to ensure that the results are rigorously tested so that errors in interpretation do not occur in critical areas of the regression and go undetected.

Sources