Decision Trees - Graphical Explainable AI • Aggregata

Classification

In the last decade the topic Machine Learning became ever larger. The goal of all this was to be able to automate decisions or optimize processes. Beside the success of different “Machine Learning” algorithms however problems in the understanding of such algorithms came up. Such an algorithm, which corresponds to this condition, is the algorithm of the Decision Trees.

Definition of Decision Trees

Decision trees are a decision support tool that contains a tree-like model with different decisions and their corresponding results, costs and other information. Decision trees are often used in decision analysis to find an optimal strategy which achieves a certain goal under given criteria (e.g. cost minimization). ¹ ²

Furthermore, it is an important tool in the field of [Explainable Artificial Intelligence]. Explainable Artificial Intelligence is mainly about making decisions of a machine learning model understandable for the user - a property which neural networks do not have in principle. ³

A decision tree consists of different nodes and branches. Each decision tree begins in its structure with a root node, which represents the initial state in the decision sequence. This then splits into at least two branches, which represent the decision. At the end of each branch there is again a node, which represents the initial state after the corresponding decision. In this way it is possible to work through the complete sequence of decisions and to build up a tree structure and a tree structure can be built up and all exits of the decisions can be modeled. At the end of the decision tree there are then the Terminal Nodes, which are represent a final classification or regression. ⁴

Often a parent node (before the decision) is called a Parent Node, and the decision then results in a Child Node.

Tasks, which can be processed with decision trees, are for example a classification or to a limited extent also regressions.

Advantages of decision trees

A number of advantages speak especially for the application areas mentioned above: ² ⁴

easy interpretability: the true/false logic of the decision tree are generally very simple to understand, furthermore the structure helps with clear direction of the decisions.
little preparation of data necessary: Decision trees are very easy to generate from data sets. Algorithms for generating decision trees are basically able to handle different variables (discrete, continuous).
great flexibility: decision trees are suitable for use in both classification and regression.

Disadvantages of decision trees

A number of disadvantages come into play with the implementation of decision trees: ² ⁴

susceptible to overfitting: When accurately fitting the data on the label, the problem often arises that the decision tree fits very well on the specialized training data, but in reality does not generalize well enough.
High Variance Estimators: Small changes in the data can result in completely different decision trees.
computer intensive generation: decision tree generation algorithms require a lot of time and computer resources to generate the appropriate decision trees on the data sets.

Building a decision tree

Often one will have a certain data set with several input variables and want to generate a classification on the basis of the data. Thus at the beginning only the initial node with no restrictions is given, gradually the decision tree is to be generated here. For this, criteria are necessary to generate splits in the data sets, which find optimal decisions for a classification.

In order to consider meaningful splitting criteria, the notion of entropy is necessary beforehand.

Entropy

Entropy is a term in information theory that measures the inhomogeneity or impurity of a sample. It is defined as

$E(S) := - \sum_{c \in C} p(c) log_2(p(c)).$

Here $S$ represents the data set, $c$ the classes from $S$ , and $p(c)$ the ratio of the data in class $c$ to the total data points.

The values of entropy are restricted to $E(S) \in [0, 1]$ . If all data points from the dataset belong to a single class, then the entropy automatically becomes zero. This follows from the fact that there is no impurity left in this case. As a goal of our decision tree it is thus derivable that in the terminal nodes thus if possible an entropy of zero should be present.

Alternatively, the Gini Impurity can be defined:

$G(S) := 1 - \sum_i (p_i)^2.$

Equivalent to entropy, this should run towards zero if possible.

Splitting Criterion

To split the data accordingly, you could use the Information Gain, which is defined as follows:

$I(S, a) := E(S) - \sum_{v \in values(a)} \frac{\vert S_v \vert}{\vert S \vert} E(S_v).$

The set $S_v$ is defined as $S_a(v) := \{ x \in S: x_a = v \}.$ ⁵

The information gain describes the difference in entropy before and after the split. The goal is to minimize the entropy after the split so that the information there is as homogeneous as possible.

Pruning

With the generation of relatively exact decision trees often the problem arises that these are very large and thus the resulting decisions are connected with many small steps and the decisions are no longer necessarily clearly comprehensible. To avoid this, the concept of Decision Tree Pruning exists, which is supposed to shorten the length of the decision tree.

The idea is to “prune” sections and non-critical branches of the tree without having a large loss of precision in the underlying task. This method is mostly applied to already generated decision trees.

The problem here is that it is not clear how large the corresponding tree will later become without generating large errors on the data set. A tree that is too small may not be able to correctly estimate certain nuances of the data set, while trees that are too large usually suffer from overfitting. Thus, this is an optimization problem that arises from the nature of the project or task. ⁶

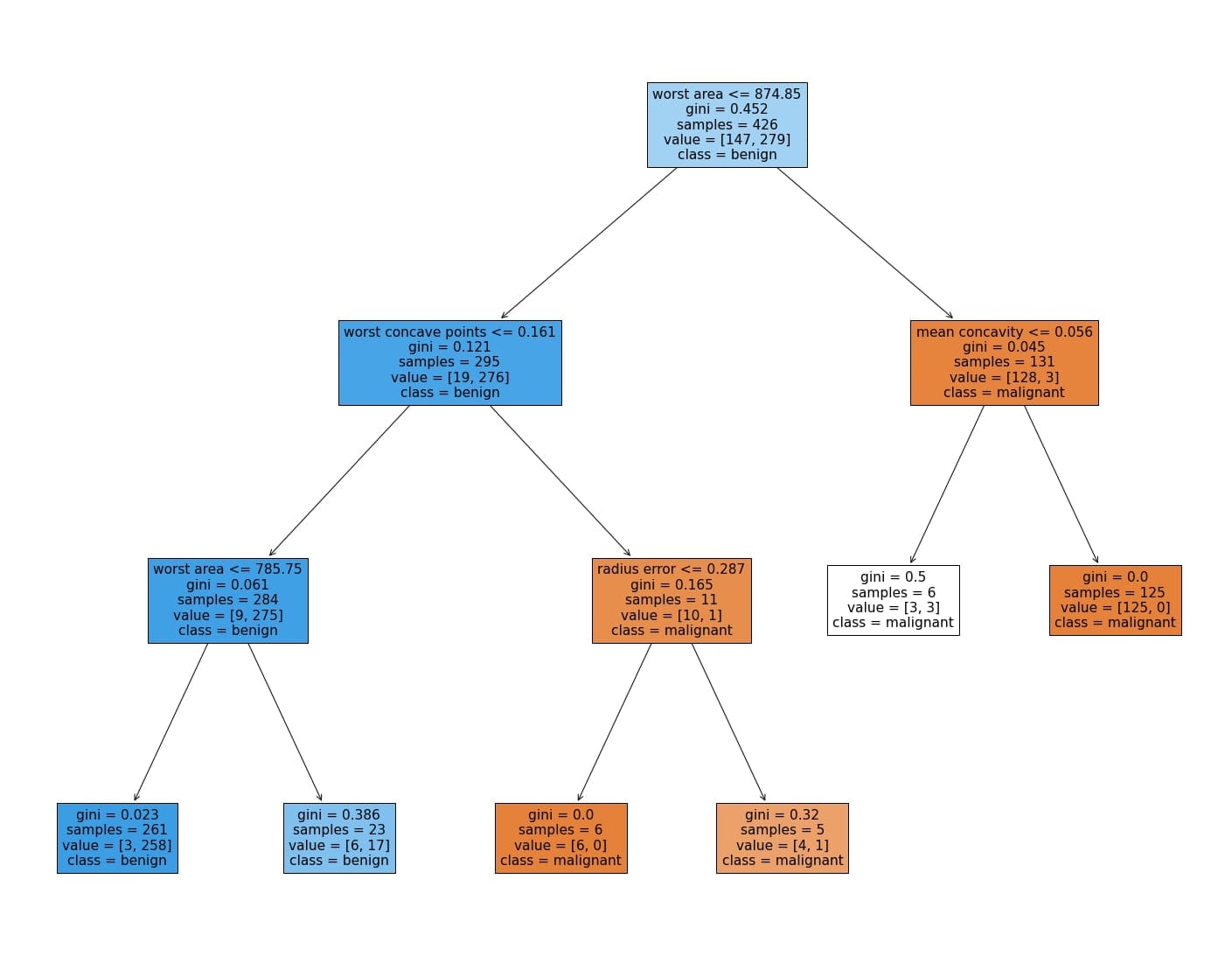
Application example

A Decision Tree Classifier can be trained from the Breast Cancer Investigation Dataset. A generated decision tree can be found below.

Decision tree generated from breast cancer dataset