Deep Q Network - Deep Learning and Reinforcement Learning in a simple way

Classification

For many years, researchers have been working on solving reinforcement learning tasks. One of the first algorithms to emerge from research in the field of Deep Reinforcement Learning was the Deep Q-Network (DQN for short). ¹ Later, this algorithm was also used by Deepmind to play on Atari games and produce comparable or better performance than humans. ^{2 3}

Mathematical basics

Concept of the Deep Q-Network

For an introduction to the terminology of “reinforcement learning” problems, this web page can be recommended.

The idea of the Deep Q-Network is to learn and choose the action at each step of the environment with which the maximum return is associated. The return is defined as

The return is sometimes referred to as expected return or discounted reward.

Here $\gamma \in (0, 1)$ represents the discount factor and $r_t$ the reward by the environment in time step $t$. The discount factor is a quantity that represents how long and strong rewards have an effect on the return.

For $\gamma \rightarrow 1$ rewards always stay in the return and do not decay, for $\gamma \rightarrow 0$ rewards relalistically have an effect on the return only for a few (or extremely: one) time step.

Due to the fact that the neural network tries to approximate a return, one can speak here of a function approximator instead of the neural network. This is because the neural network tries to learn the best possible rewards for all possible actions depending on the observation. So one can call the neural network a

where $S_i, i=1, \cdots, n$ are the sets of different observations (for example, different angles for robots) and $A_j, j=1, \cdots, m$ are the sets of different actions (for example, move arm 1 or 2).

Update formula

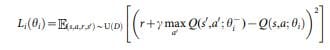
In this formula it can be seen that one tries to minimize the loss function $L_i(\theta_i)$ with the network parameters $\theta_i$ of the Deep Q-Network. This is attempted via Mean Squared Error. Classically, this is done not only in the current step, but also via an Experience Replay $D$. ^{4 5 6}

The Experience Replay contains old and new runs of episodes. It is intended to prevent the network from going through Catastrophic Forgetting; that is, the network forgets any progress it has made. There are a number of other functionalities implemented in later algorithms that also try to prevent catastrophic forgetting.

For this purpose, information about old runs is sampled (usually via a discrete uniform distribution of the indices), whereby in general no episodes but steps are extracted. An alternative to this can be found in Possible improvements.

Sampling from Experience Replay has the advantage of decoupling information between several different episodes, usually resulting in better training behaviors. In addition, one also keeps more information per training episode (especially early episodes in training when there are many environments) due to more steps considered in the environment, which increases the quality of the computed gradient. This can be detrimental if the current best step depends on the previous steps; however, Deep Q-Networks are generally not very good in such environments due to poor information merging between multiple steps. Here, one usually uses n-step agents such as the Deep Recurrent Q-Network.

Furthermore, Reward Clipping is used, which transforms $r_t$ to $r_t' \in [0, 1]$ using a linear transformation. This avoids two problems:

1. Neural networks require many learning steps to build weights to generate large values with acceptable error tolerance. If the reward is reduced, this speeds up training.

2. Environments with different sized rewards (for example: at the beginning $\approx 1$, later $\approx 30$) are more unstable. Reward clipping prevents this problem from occurring.

Implementation using Tensorflow

Problem

In this implementation, the agent will try to solve OpenAI’s CartPole problem. A categorical policy is used here. For more agent training environments, see here.

Pseudocode

Code

We start with all the necessary imports:

import datetime
import math
import gym

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

from collections import deque
from tensorflow.python.keras.models import Sequential
from tensorflow.python.keras.layers import Dense, InputLayer
from tensorflow.python.keras.optimizer_v2.adam import Adam

It should be noted that this implementation was tested with a Tensorflow version of 2.9.1. For lower versions, the imports may need to be changed from import tensorflow.python.keras.[...] to import tensorflow.keras.[...].

First, the experience memory is implemented.

class ExperienceMemory:
    def __init__(self, memory_length: int=10000, batch_size: int=64, nonunique_experience: bool=True):
        self.memory_length = memory_length
        self.batch_size = batch_size
        self.nonunique_experience = nonunique_experience

        # ** Initialize replay memory D to capacity N **
        self.cstate_memory = deque([], maxlen=self.memory_length)
        self.action_memory = deque([], maxlen=self.memory_length)
        self.reward_memory = deque([], maxlen=self.memory_length)
        self.done_memory = deque([], maxlen=self.memory_length)
        self.pstate_memory = deque([], maxlen=self.memory_length)

    def record(self, cstate, action, reward, done, pstate):
        # Convert states into processable objects
        cstate = tf.expand_dims(tf.convert_to_tensor(cstate), axis=0)
        pstate = tf.expand_dims(tf.convert_to_tensor(pstate), axis=0)

        # Save data
        self.cstate_memory.append(cstate)
        self.action_memory.append(action)
        self.reward_memory.append(reward)
        self.done_memory.append(done)
        self.pstate_memory.append(pstate)

    def return_experience(self):
        # Retrieve experience
        batch_indices = np.random.choice(len(self.cstate_memory), size=self.batch_size, replace=self.nonunique_experience)
        batch_cstate = np.array(list(self.cstate_memory))[batch_indices, :]
        batch_action = np.take(list(self.action_memory), batch_indices)
        batch_reward = np.take(list(self.reward_memory), batch_indices)
        batch_done = np.take(list(self.done_memory), batch_indices)
        batch_pstate = np.array(list(self.pstate_memory))[batch_indices, :]

        # Convert experience into respective tensorflow tensors
        cstates = tf.squeeze(tf.convert_to_tensor(batch_cstate))
        actions = tf.convert_to_tensor(batch_action)
        rewards = tf.convert_to_tensor(batch_reward, dtype=tf.float32)
        dones = tf.convert_to_tensor(batch_done, dtype=tf.int64)
        pstates = tf.squeeze(tf.convert_to_tensor(batch_pstate))

        return (cstates, actions, rewards, dones, pstates)

    def flush_memory(self):
        self.cstate_memory.clear()
        self.action_memory.clear()
        self.reward_memory.clear()
        self.done_memory.clear()
        self.pstate_memory.clear()

The experience memory represents a simple container for memories of past transitions. With return_experience we additionally adjust the dimensionality of the output, so that the model accepts this later without problems.

Now we write our class DQNAgent. This contains the functions __init__, compute_action, update_epsilon_parameter, store_step, get_batch and train:

class DQNAgent:
  def __init__(self, observation_size, action_size):
    self.observation_size = observation_size
    self.action_size = action_size

    # Network parameters
    self.memory_length = 26000
    self.alpha = math.pow(10, -3)
    self.gamma = 0.951
    self.epsilon = 0.8
    self.min_epsilon = 0.05
    self.epsilon_decay = 0.005
    self.batch_size = 64
    self.nonunique_experience = True

    # ** Initialize replay memory D to capacity N **
    self.experience_memory = ExperienceMemory(self.memory_length, self.batch_size, self.nonunique_experience)

    # ** Initialize action-value function Q with random weights **
    self.model = Sequential([
            InputLayer(input_shape=self.observation_size, name="Input_Layer"),
            Dense(units=128, activation='relu', name='Hidden_Layer_1'),
            Dense(units=self.action_size, activation='linear', name='Output_Layer')], name="Deep_Q-Network")
    self.model.compile(loss="mse", optimizer=Adam(learning_rate=self.alpha))
    # self.model.compile(loss='categorical_crossentropy', optimizer = Adam(learning_rate=self.alpha1))
    self.model.summary()

    # Define metrics for tensorboard
    self.score_log_path = 'logs/' + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
    self.score_writer = tf.summary.create_file_writer(self.score_log_path)

The comments in this function are relatively self-explanatory. The constructor requires the dimensionality of the input and output values, which are later used to initialize the first and last layers of the neural network. The hyperparameters are derived from experience and various hyperparameter optimizations; changing the model may require a different configuration of the hyperparameters. Furthermore, the Experience Replay is initialized and an I/O object for Tensorboard is created, which visualizes the training process. For Tensorflow Tensorboard is one of the best packages to display metrics during the training process.

Many blogs also refer to Seaborn or Matplotlib in this regard. Matplotlib always proved to be a simple and robust tool for visualizations of any kind, Seaborn advertises to be the more modern successor of many statistical visualization tools.

Deque is a dynamic array, which has a certain maximum length. If entries are added after reaching the maximum length, the last entries are replaced by the new entries.

  def compute_action(self, observation, evaluation: bool=False):
    if (np.random.uniform(0, 1) < self.epsilon and evaluation == False):
      return np.random.choice(range(self.action_size)) # ** With probability epsilon select a random action a_t **
    else:
      observation = np.expand_dims(observation, axis=0)
      Q_values = self.model([observation])
      return np.argmax(Q_values) # ** Otherwise select a_t = argmax(Q) **

  def update_epsilon_parameter(self):
    self.epsilon = max(self.epsilon * math.exp(-self.epsilon_decay), self.min_epsilon)

We continue with the function for selecting the action under the current observation. Here an Epsilon Greedy Scheme is used, which selects with probability $\epsilon \in [0, 1]$ a random action, with probability $1 - \epsilon$ the action is selected by the network. This scheme serves the dilemma between exploration vs exploitation, which is authoritative in reinforcement learning. During training, $\epsilon$ should gradually decrease without falling below a threshold $\epsilon_{min}$. This is guaranteed by the update_epsilon_parameter function here. The function compute_action has the additional argument evaluation: bool=False here, which controls the activity of the epsilon greedy scheme.

  def store_step(self, cstate, action, reward, done, pstate):
    self.experience_memory.record(cstate, action, reward, done, pstate)

Next comes the function that interacts with the Experience Replay. The method store_step gets a tuple of all information per time step (and the observation of the following step) and stores it in the Experience Replay. In this case, a direct interface could also be implemented, but this represents a more general interface. This can be modified internally if needed, without having to adapt surrounding code further (as for example later with the training loop).

  def train(self): # **For each update step**
    # ** Sample random minibatch of transitions from D**
    b_cstate, b_action, b_reward, b_done, b_pstate = self.experience_memory.return_experience()

    # ** Set y_j **
    prediction_model_p = self.model(b_pstate)
    q_value_network = np.zeros((self.batch_size,))

    b_done = b_done.numpy()
    max_pred = np.max(prediction_model_p, axis=1)
    q_value_network = (1 - b_done) * self.gamma * max_pred
    target_q_p = np.add(b_reward, q_value_network)

    # **Perform gradient descent step on Q**
    self.model.train_on_batch(b_cstate, target_q_p)
    # self.model.fit(b_cstate, target_q_p, verbose=0)

Here comes the heart of the actual algorithm. In this method, we update the network based on some of the information we have gathered during the training. This function is the implementation of the update step in the pseudo code. Below, the line self.model.fit(b_cstate, target_q_p, verbose=0) is commented out, because mostly the method self.model.train_on_batch(b_cstate, target_q_p) turned out to be a better training method. It is possible that multiple epochs will also give better results on this, currently the network only trains on one episode.

def training_loop(env, agent: DQNAgent, max_frames_episode: int):
  current_obs, _ = env.reset()

  episode_reward = 0
  for j in range(max_frames_episode):
    action = agent.compute_action(current_obs)

    next_obs, reward, done, _, _ = env.step(action)
    next_obs = np.array(next_obs)
    agent.store_step(current_obs, action, reward, done, next_obs)

    current_obs = next_obs
    episode_reward += reward

    if done:
      agent.update_epsilon_parameter()
      break

  return episode_reward, agent

def evaluation_loop(env, agent: DQNAgent, max_frames_episode: int):
  current_obs, _ = env.reset()
  evaluation_reward = 0
  for j in range(max_frames_episode):
    # ** Execute action a_t in emulator and observe reward r_t and image x_{t+1}
    action = agent.compute_action(current_obs, evaluation=True)

    next_obs, reward, done, _, _ = env.step(action)
    next_obs = np.array(next_obs)

    # **Storing all information about the last episode in the memory buffer**
    agent.store_step(current_obs, action, reward, done, next_obs)

    # Reseting environment information so that next episode can handle the previous information
    current_obs = next_obs
    evaluation_reward += reward

    if done:
      break

  return evaluation_reward, agent

The two functions for training and validating the learning progress follow. The function training_loop is only meant to be repeated over and over again to provide more information to the agent as it “moves” through the environment.

Note: In this implementation there is no update step after each time step, but after each episode.

The function evaluation_loop basically does nothing else, except that this one does not involve exploration.

n_episodes, max_frames_episode, avg_length, evaluation_interval = 5000, 500, 50, 10
episodic_reward, evaluation_rewards = [], []

env = gym.make("CartPole-v1")
n_actions = env.action_space.n
observation_shape = env.observation_space.shape[0]

tf.random.set_seed(69)
np.random.seed(69)

agent = DQNAgent(observation_shape, n_actions)
eval_reward, episode_reward = 0, 0

# agent.score_writer.init()
for i in range(n_episodes):
    # **Observing state of the environment**
    episode_reward, agent = training_loop(env=env, agent=agent, max_frames_episode=max_frames_episode)

    print("Training Score in Episode {}: {}".format(i, episode_reward))

    if (i % evaluation_interval == 0):
      # Evaluation loop
      eval_reward, agent = evaluation_loop(env=env, agent=agent, max_frames_episode=max_frames_episode)
      print("Evaluation Score in Episode {}: {}".format(i, eval_reward))

    with agent.score_writer.as_default():
      tf.summary.scalar('Episodic Score', episode_reward, step=i)
      if (i % evaluation_interval == 0):
        tf.summary.scalar('Evaluation Score', eval_reward, step=i)

    episodic_reward.append(episode_reward)
    agent.train()

Here you will find the initialization of all necessary parameters for the training loop and the training loop itself. Seeds were used here so that the training is reproducible, this should be removed in an enterprise environment to keep the possible results flexible. Furthermore you can see here the write operations of Tensorboard. Depending on the system, it may be necessary to initialize the writer. Mostly, however, this should work without this initialization. A visualization of the training performance follows:

Here you can see that within 1000 episodes ($\approx 7$ minutes CPU time) the performance of the model has improved compared to the beginning. There is more potential regarding the performance, with more adapted architectures and even better adapted hyperparameters.

Note: Training performance can sometimes differ greatly from device to device and corresponding seeds. General reproducibility of such results cannot generally be guaranteed.

Implementation notes

1. tensorflow provides the functionality model.predict(observation) instead of model(observation). See here for this. Problematic here is that the predict function has a significantly larger runtime. So model(observation) should be used, unless there are special reasons why this should not be done.

Alternatives of this algorithm

As described in the source ², this network in its basic form has problems approximating the Q-target $y_i$. The reason is that this is not constant and so the network may exhibit instabilities in the learning process.

The paper provides a frozen target network as an extension. This is always updated every $n \in \mathbb{N}$ episode and used to compute the Q-target. The paper shows that this change leads to significantly better results than in the basic form.

Such an update of the network parameters of the Frozen Network every $n$ episodes is also called a Hard Update.

Furthermore, a comparison between the average performance of the two algorithms:

Note: Training performance can sometimes differ greatly from device to device and corresponding seeds. General reproducibility of such results can generally not be guaranteed.

An improvement in training performance would be expected here. This cannot be seen here. Despite this fact, a reduction in variance can be seen.

Implementation using Pytorch

After the detailed implementation using Tensorflow, reference is made to this website. There you can find a relatively good implementation using Pytorch, which technically should be able to reproduce the results.

Possible improvements

One way to improve the training process is to use Importance Experience Replay. Importance Experience Replay improves the process by discarding the discrete uniform distribution used to sample the information from the Experience Replay. Instead, a probability is computed for each time step in the Experience Replay, which depends on the deviation between predicted and actual return. This means that potentially important time steps for the agent are repeated more often, instead of time steps that the agent already approximates well.

Outlook

While the Deep Q-Network is no longer the most current or state-of-the-art algorithm for solving reinforcement learning problems, it provides the basis for many advanced algorithms such as D3QN or actor-critic architectures (where a DQN “scores” the observation-action pair). Accordingly, understanding this algorithm is central to advanced understanding of advanced reinforcement learning algorithms.

Sources