Artificial Neural Networks - A Milestone in Machine Learning • Aggregata

Classification

Machine Learning has gained much importance in recent years. The ability to learn autonomously using data is a promising feature for future software. One of the important supports for such software is artificial neural networks. The operation and application of these are explained below.

Idea of artificial neural networks

Basically we speak of artificial neural networks as an abstraction of biological neural networks, which are supposed to represent systems like the human brain in a simplified way. Here, a system is created from artificial neurons, which are interconnected with the help of neural connections. Classically, the biological signal (“stimulus”) is modeled as a real number. ¹

Basically, artificial neural networks are not trained for a specific task in this process, but try to adapt based on training data. Corresponding results vary afterwards with corresponding data sets. As an output result, an algorithm is modeled, which should be able to solve the corresponding task at hand as well as possible. ² ³

Artificial neurons as a mathematical operation

At the heart of every artificial neural network are the corresponding artificial neurons. These are designed to represent the corresponding biological counterpart in a simplified way. Each neuron has a set of inputs and an output. The inputs can be either classical input data or corresponding outputs from previous neurons.

To calculate the corresponding output of the neuron, one can classically multiply a weight $\vec{a}$ on the inputs $\vec{x}$ and then add the bias $\vec{b}$ to it. Then, an activation function $\sigma(\cdot)$ is applied to the result. This function determines to what extent the neuron fires, and if it fires, additionally how strong the output signal becomes. The entire operation then looks like this:

$\sigma(\vec{a}^T \vec{x} + \vec{b})$

This can be performed iteratively through all neurons. The last neurons in the network should then classically represent a representation that solves the task (for example, the probability of a class membership). ¹ ⁴ ⁵

Training then consists of the step of adjusting the values of $\vec{a}$ and $\vec{b}$ so that the output values of the network to the given values has as small a deviation as possible. There are several metrics to measure this. A list of such metrics can be found here.

Architecture

In contrast to biological neuronal networks, artificial neuronal networks are not flexible in their structure. Therefore, an architecture of layers, which contains neurons, must be given here with artificial neural networks. In the layers the outputs of the neurons are computed in parallel. A neural network with more than three layers is called a deep learning model. ⁵

Such an architecture is shown below:

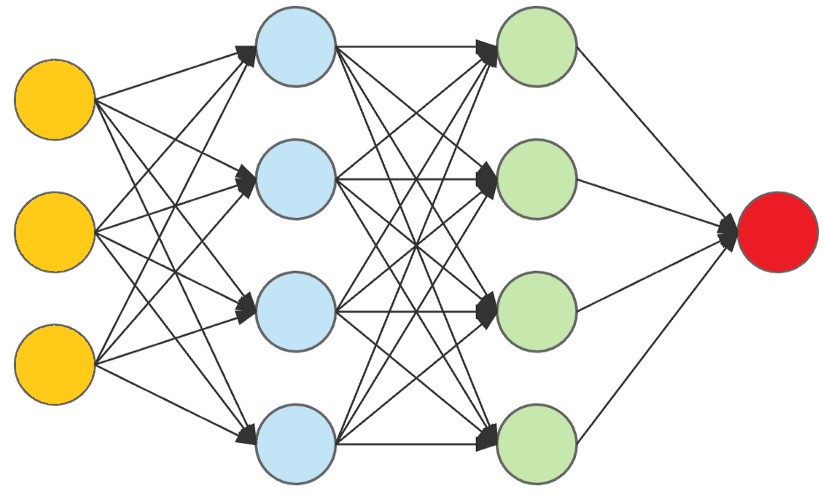
Example neural network architecture - extracted from w3school.com

Feedforward Networks

In general, we speak of feedforward networks when several layers of neurons are connected in series to achieve a certain task. The network has no loops and the input is processed from the front to the back of the network - hence the name.

Such models are classically easier to implement than other forms of neural networks, but are often only capable of processing a single input and output tensor. For an example, see here. ⁶ ⁵

Convolutional Neural Networks

Convolutional Neural Networks are neural networks that use filtering operations and pooling operations in different layers to reduce the dimensionality of the input data and better detect important features. This type of networks is mainly used in image recognition, where this type of network achieves good results. However, such networks require high numbers of neurons, which may make training take longer. ⁷ ³ ¹

Recurrent Neural Networks

Recurrent neural networks are characterized by the fact that, unlike feedforward networks, they allow loops in the network, and thus there is not always a single direction of information in the network across all layers. This allows tasks such as sequence forecasting or handwriting recognition to be predicted with fewer data points; unlike feedforward networks, in which this is more difficult to achieve. However, such networks are both slower to evaluate and to train. Among other things, this also causes problems with some optimization algorithms for the weights of the network. ⁵ ⁸ ² ³

Fields of application

Due to the property of artificial neural networks to be universal function approximators, many problems can be solved using artificial neural networks.¹

A feedforward network, which consists only as fully connected neurons, can be used as a universal function approximator according to the Universal Approximation Theorem. For this, nonlinear activation functions are necessary.

To be a universal function approximator means that a neural network constructed in this way can theoretically approximate any function exactly.

Examples are:³

image and speech recognition
application in control engineering
pattern recognition
applications concerning medical diagnosis
translation

and many more. Despite these examples of applications, there are still a number of problems which should be considered:

the universal approximation theorem is unfortunately not constructive; it is unclear what network parameters such as number of layers, number of neurons or other parameters should have for values,
convergence: neural networks are susceptible to local minima of the loss function; some optimization methods cannot guarantee convergence beyond a certain distance to a local/global minima.
neural networks may require large amounts of data and computational power to perform well.
neural networks are subject to the problem that the evaluation of erroneous results is complex. In particular, it is unclear which values the neural network will output for data points that are not present in the data set - however, these are often used in practice and it is not possible to test all values in this case.

All in all, many of the theoretical properties and problems are important, but in reality they play only a limited role. Also small neural networks achieve in many areas already good results and are therefore often applicable.